1、圆的弧长计算

s=rθ

C=2πr=πd

式中：

s一一圆的弧长；

θ一一圆弧角度（角位移）；

C一一圆的周长；

r一一圆弧的半径；

d一一圆弧的直径；

2、旋转运动的三个测量值：角位移、弧度（rad）、公转（r）

1r（公转）=2π（rad 弧度）=360°（角位移）

1rad=360°/（2π）=57.3°

1°=2π/360°=

1rad=0.16r

1°=0.003r

注：弧度是没有单位的。

例如：

100r/min=100x2π=626rad/min

100r/min=100x360°=3600°/min

3、线速度与角速度之间的关系

角速度是角度（角位移）的变化率

s=rθ

ω= θ/t

v=s/t=rθ/t=rω（线速度（圆周速度）与角速度之间的关系）

其中s/t为圆周（切向）速度

式中：

s一一圆弧的周长；

r一一圆弧的半径；

θ一一圆弧角度 ；

t一一时间；

ω一一角速度；

v一一圆周速度（切向速度）

角速度的单位一般是rad/s，工程实际旋转速度的单位一般用r/min（每分钟转多少转）

例如：

ω=10.5rad/s=10.5x60/（2π）=100r/min

4、转速

n=ω60/（2π）

式中：

n一一转速，r/min；

ω一一角速度，rad/s；

同样

ω=n 60/（2π）

式中：

ω一一角度度，rad/s；

n一一转速，r/min

综合：线速度=切线速度=圆周速度

v=rω=rn60/（2π）

或v=n（2πr）=n（πd）

注意单位统一。

例如：

滚筒线速度为100r/min，滚筒半径为10cm，求线速度是多少？

v=n（2πr）=100x（2πx10）=6283cm/min

5、功率

功率是力与速度的乘积。

功是力与在该力下所产生的位移的乘积。

牛顿第二定律

F=ma

式中：

F一一力，N；

m一一质量，kg；

a一一加速度，m/s^2。

P=Fv

式中：

P一一功率，W（瓦特）；

F一一力，N；

v一一速度，m/s。

W=Fd

式中；

W一一功（力F所作的功）J(焦耳）（1J=1N*m）；

F一一力,N；

d一一位移,m。

E=（1/2）mv^2

式中：

E一一能量（动能），J（焦耳），N*m，W*s；

m一一质量,kg；

v一一速度,m/s。

g=9.81m/s^2

1kg*m^2/s^2=1(kg*m/s^2)*m=1ma*m（牛顿第二定律）=1F*m=1N*m

6、旋转运动

T=Fr

式中：

T一一转矩，N*m；

F一一力，N；

r一一半径，m。

P=Tω

式中：

P一一功率，W（瓦）；

T一一转矩，N*m；

ω一一角速度，rad/s。

W=Tθ

式中：

W一一功，J(焦耳），N*m，W*s ；

T一一转矩，N*m；

θ一一角位移，rad。

E=（1/2）Jω^2

式中：

E一一能量，J，N*m，W*s；

J一一转动惯量，kg*m^2；

ω一一角速度，rad/s。

Ta=Jα （类似于直线运动的牛顿第二定律 F=ma）

式中：

Ta一一加速度转矩，N*m；

J一一转动惯量，kg*m^2；

α一一角加速度，rad/s^2。

7、转动惯量的折算

JR=JL/N^2

式中：

JR一一反映到电机轴上的惯量；

JL一一负载惯量；

N一一减速比。

转动惯量的折算依据：折算前后动能相等。

转动惯量的大小反映出各传动机构所储存的机械惯性的大小，即所储存动能的大小。

工作部分机构的质量所产生的动能折算到电动机轴上，需要在电动机轴上用一个转动惯量为J的转动体与之等效。

所以各个传动部件的转动惯量折算的电机轴上，应该除以电动机与该级转速比（减速比）的平方。

8、斜面

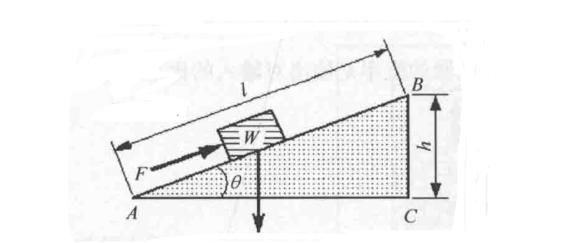若不计摩擦，则

F=Wsinθ

sinθ=高度h/长度l

式中：

F一一外力，N；

W一一负载，N；

θ一一斜面与水平方向的夹角，度（°）。

9、螺旋千斤顶

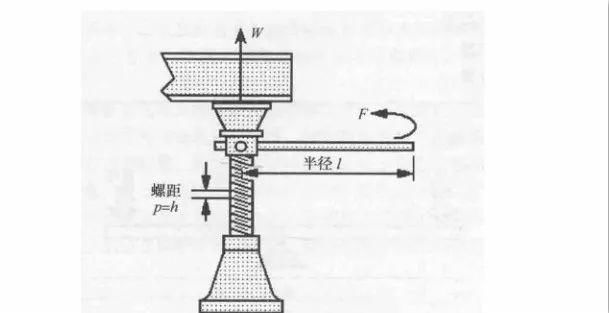千斤顶的螺旋部分可以看成是一个斜面沿着圆柱缠绕。力F必须作用在水平放置的、长度为l的杆的末端。杆必须必须转动一圈或走过一个周长s=2πl的圆，载荷才能升高h，即升高螺旋部分的一个螺距p。

则：

F=Wh/s=Wp/（2πl）

式中：

F一一外力，N；

h一一移动距离（上升高度），m；

s一一周长（斜面长度），m。

觉得文章不错，就点个在看吧

文章来源：《机械设计与研究》 网址: http://www.jxsjyyj.cn/zonghexinwen/2021/0522/965.html